
https://www.acmicpc.net/problem/10870
10870번: 피보나치 수 5
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
기존에 활용했던 재귀함수를 사용하면 이렇게 표현할 수 있다.
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
n = int(input())
print(fibonacci(n))문제에서 주어진 0 =< n =<20 범위 내에서는 탈없이 작동됐지만 수가 커질수록 연산 시간이 기하급수적으로 커지게 된다.

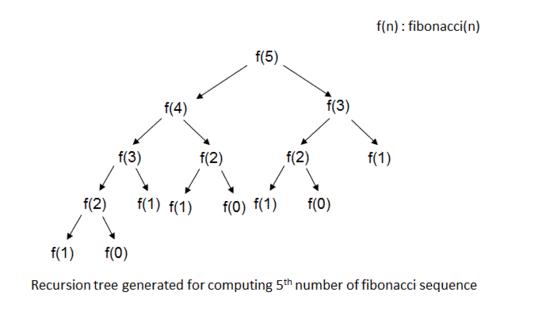
그림에서 설명하듯이 n-1을 연산하는데 쓴 동일한 작업을 n-2에서도 반복하는 비효율적인 방식으로 연산하기 때문.
동적 프로그래밍(Dynamic Programming) - 메모이제이션(memoization) 활용
메모이제이션 - 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 동적 프로그래밍의 핵심이 되는 기술이다.
쉽게 말해 수식을 돌리면서 키와 밸류값을 저장해놓는 딕셔너리를 생성해, 이전단계인 경우 메모에서 값을 불러오는 식으로 시간을 단축시키는 것.
내 제출
# memo 라는 변수에 Fibo(0)과 Fibo(1) 값을 저장
memo = {
0: 0,
1: 1,
}
# 기존 재귀함수는 계속 n-1 n-2를 같은 연산을 해가면서 풀었음
# 만약 메모에 있으면 그 값을 반환하고
# 없다면 수식대로 구한다
# 다시말해 딕셔너리에 f(1) f(2) f(3) .... 값을 저장해서 불필요한 재연산 없애기
def fibo_dynamic_programming(n, fibo_memo):
if n in fibo_memo:
return fibo_memo[n]
nth_fibo = fibo_dynamic_programming(n - 1, fibo_memo) + fibo_dynamic_programming(n - 2, fibo_memo)
fibo_memo[n] = nth_fibo
return nth_fibo
print(fibo_dynamic_programming(int(input()), memo))
